Transformer

I recently did a project on Speech recognition(link). The project was done trying to imitate the DeepSpeech2 model and incorporating further advancements on the field. Halfway through the project, I stumbled upon attention and shortly after that on transformer networks. I have already written about attention(previous) and here I'm trying to write about transformer networks and how I try to visualize/understand them.

Recurrent Neural networks are great and with Gated Algorithms(LSTMS) they solve vanishing gradient problem to some extent, but it was never quite like how humans pay attention to things(well from my perspective). We don't memorize things, we just pay attention to some things more than others. Also the fact that RNNs, recursive by nature can't utilize the power of GPUs.

So, here comes the transformer

This image is probably to much so, let's first look at the Embedding layer of the input Source. Further, to visualize better let's take a phrase; a phrase from the godfather:

I'm gonna make him an offer he can't refuse

Say, our model takes the first phrase as an input and it has to predict or more specifically generate the second phrase.

Initially, the words in the sentence need to be represented in some format as the algorithm(computer) cannot understand a word. The words are represented as a matrix where each dimension of the word gives some linguistic feature of the word

Eg.

For the word Man, the embedding representation could be (if represented in 4 dimensions, usually its around 300):

Tensorflow embedding projector has an excellent representation of the embedding matrix (https://projector.tensorflow.org/)

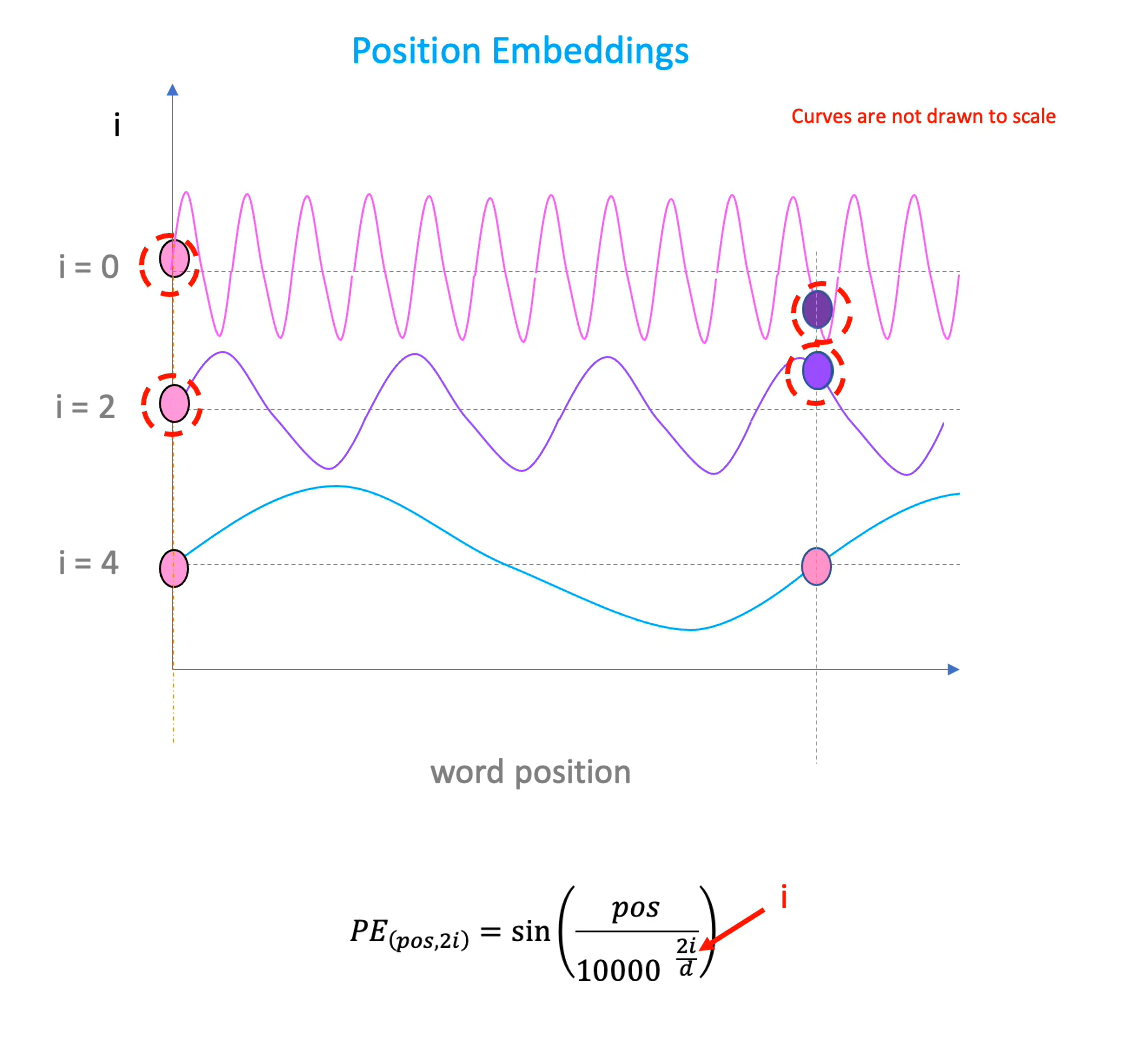
Now, that we have the words represented as embedding matrices, a new problem arises. For our sentence, we need to determine the position of each word. LSTMs had it easy, they sequentially took in the input but in this case, the position of each word in the sentence needs to be determined. So, we create a positional matrix and add it to our embedding layer. What exactly is the positional embedding?

Why this and not others.... probably some other time. But what does this equation mean?

1. $pos$ represents the position of the embedding on the sequence
2. $i$ represents the position inside the embedding matrix(in the man example, the value 0.4 has i of 1)
3. $d$ represents the total size of the embedding vector.(in the man example, d = 4)

What does this accomplish?

If we plot a sinusodial curve by varying the variable indicating word positions ($pos$) on the x-axis, we get a smooth looking curve. From the sinusodial curve, we use the word's height as a proxy to word positions (relative value on y-axis). For some words, the positional embeddings could have the same height(imagine the sine curve eg, 0 and 2$\pi$ fall on the same position). This problem is overcomed as there is a varying value of $i$. If we plot a curve again with a different value of i, we get the two values at a different position. So, if two points are close by on the curve, they will be similar on the higher frequencies too. it is only at higher frequencies that they have different values. We add this with our embedding matrix and we've got our positional embedding.

Multi Head Attention

In a sentence, we judge the word by looking at the context in which it appears. Multi-head attention tries to do the same.

The difference between simple attention and self attention is that simple attention selectively focuses on words with respect to a query. Self attention on the other hand also takes the relationship among words within the same sentence into account.

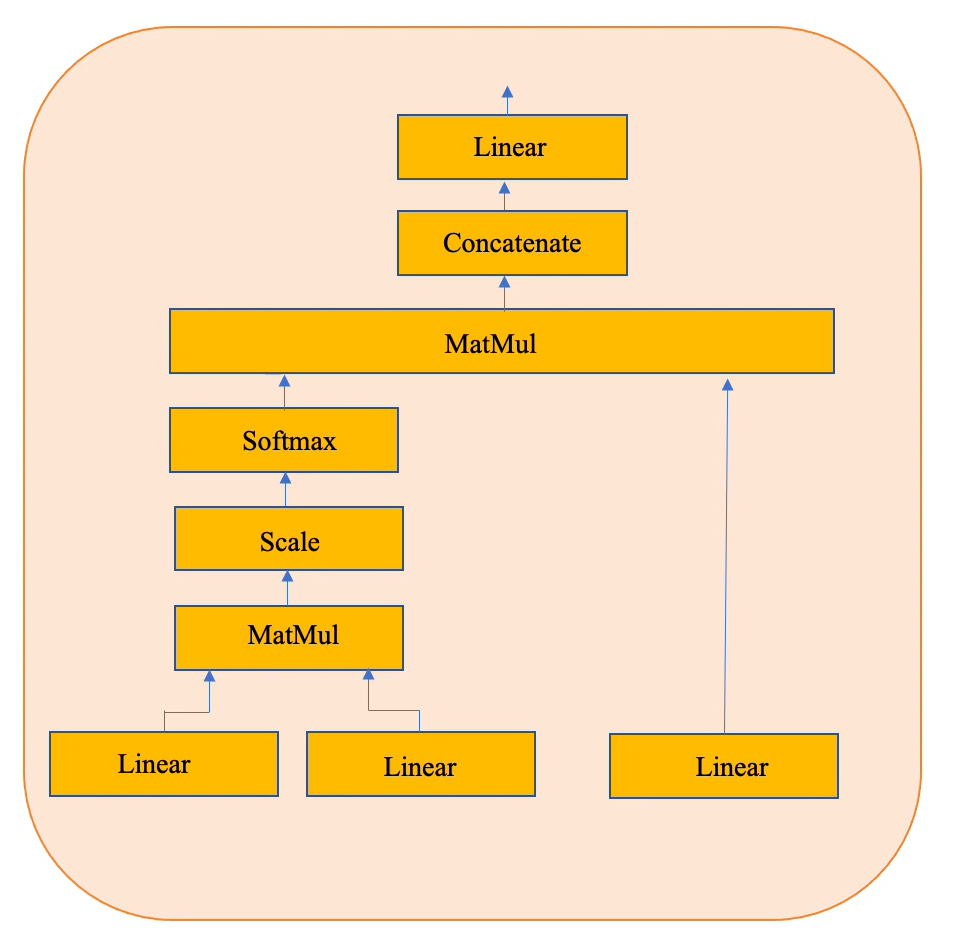
As this is self attention, all the three linear layers are fed the copies of positional embedding. The three linear layers are namely

1. Query
2. Key
3. Value

The above mentioned operations are done on Query and Key and then softmaxed. This computes the similarity between the Query and a Key (cosine similarity).

$scaling = \sqrt{d_k}$

This new matrix can be thought as a filter for the attention(attention filter). This filter when multiplied with our original embedding(passed under the linear layer) creates a new matrix with attention weights passed into it.

For the intution of this, let's take a computer vision example:

Say we have a potrait,

We don't process the image looking from the top left and then go sequentially to the bottom right of the picture. Instead we pay attention to Obama's face and after that probably the US flag behind it. The attention filter accomplishes this by filtering the required embeddings(pixels in this case). As attention is to be payed to multiple things, there are multiple attention filters. All those are then concatenated and then passed into a linear layer for the output of the Transformer Encoder.

If you've read this far, you probably already know about Residual Connections, Dense Layers, Activation Functions, Loss Functions, Backpropagation, Layer Normalization etc

Decoder

In the decoder part, same type of positional embedding is done in the beginning. The decoder generates a Start token in the beginning . It undergoes positional encoding similar to the encoder part of the network. After that, this encoding goes to the Masked Multi-Head Attention layer. The masked multi-head attention comes to fruition during the training phase of the algorithm. During training, the model is provided with both the source dialogue as well as the latter completion dialogue(target dialogue). A masking layer is applied to the Attention filter(-inf to the future values). Once this passes through the softmax layer, all the negative infinity values become 0 so our model pays 0 attention to the words of the future.

The next Multi-Head Attention layer of the decoder works fairly the same way the encoder part works but in this case, the the Key and the query come from the Encoder while the Value comes from the decoder. The layers after this point are fairly intutive and a new value is sent to the end Decoder-Fully connected layer. This layer has the dimension of the vocabulary and the word with the highest probability is selected as the output. And at the end, this decoder generates the end token which concludes the sentence.